Growth Standards

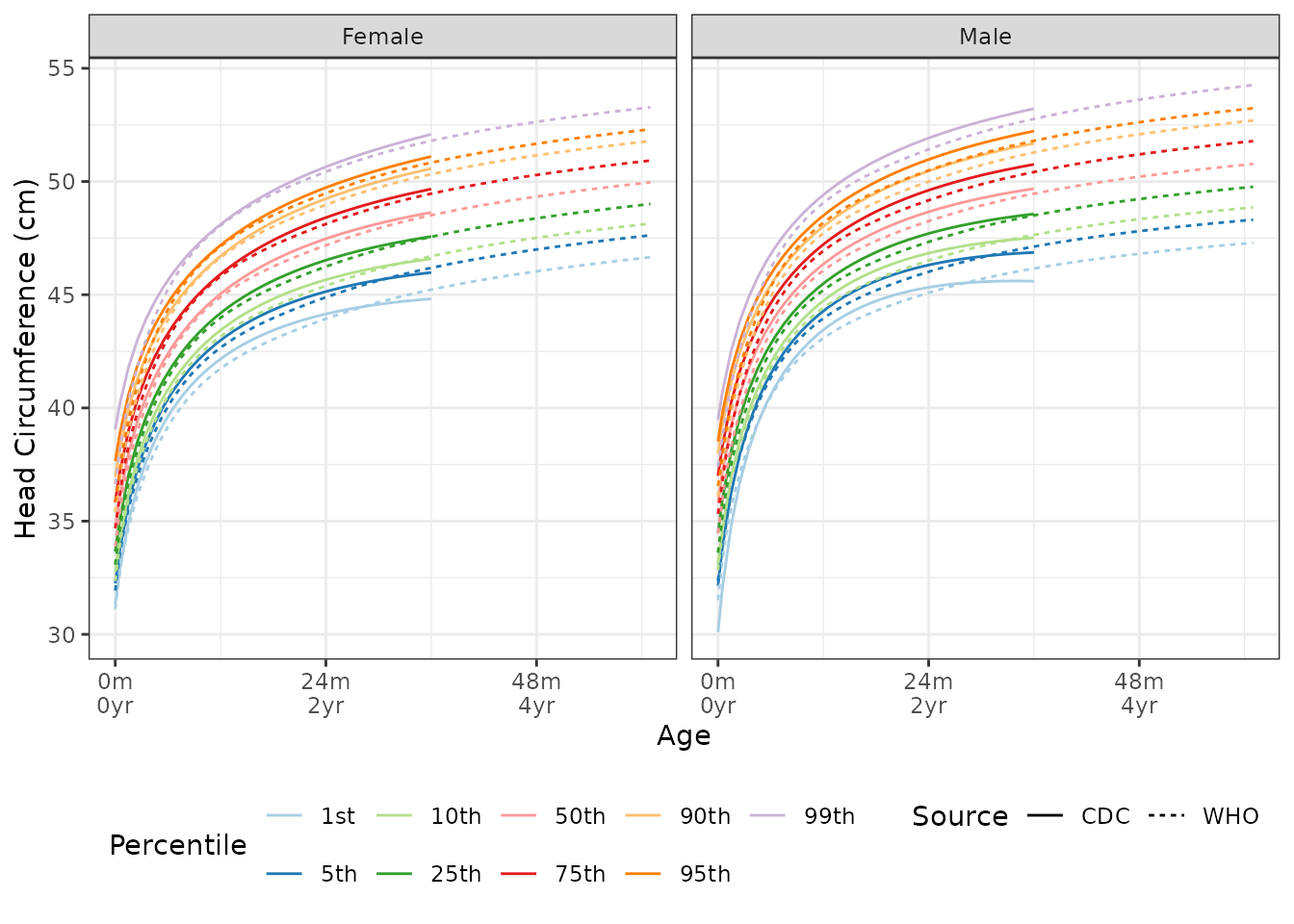
Growth Charts

Using the Percentile Data Files with LMS values provided by the CDC, and Child Growth Standards provided by the World Health Organization (WHO), we provide tools for finding quantiles, percentiles, or z-scores, for:

BMI for age,
head circumference for age,
stature for age,
weight for age, and 5, weight for stature.

All lengths/heights are in centimeters, ages in months, and weights in kilograms. Stature is used to refer both height and length; Specific methods are provided for each.

Method - LMS

All methods use the published LMS parameters to define z-scores, percentiles, and quantiles for skewed distributions. L is a $\lambda$ parameter, the Box-Cox transformation power; $M$ the median value, and $S$ a generalized coefficient of variation. For a given percentile or z-score, the corresponding physical measurement, $X,$ is defined as

$X = \begin{cases} M \left(1 + \lambda S Z \right)^{\frac{1}{\lambda}} & \lambda \neq 0 \\ M \exp\left( S Z \right) & \lambda = 0. \end{cases}$

From this we can get the z-score for a given measurement $X:$

$Z = \begin{cases} \frac{\left(\frac{X}{M}\right)^{\lambda} - 1}{\lambda S} & \lambda \neq 0 \\ \frac{\log\left(\frac{X}{M}\right) }{ S } & \lambda = 0. \end{cases}$

Percentiles are determined using the standard normal distribution of z-scores.

For all eight of the noted methods we provide a distribution function, quantile function, and function that returns z-scores.

All the growth standard functions have a quantile, percentile, and z-scores version.

BMI for Age

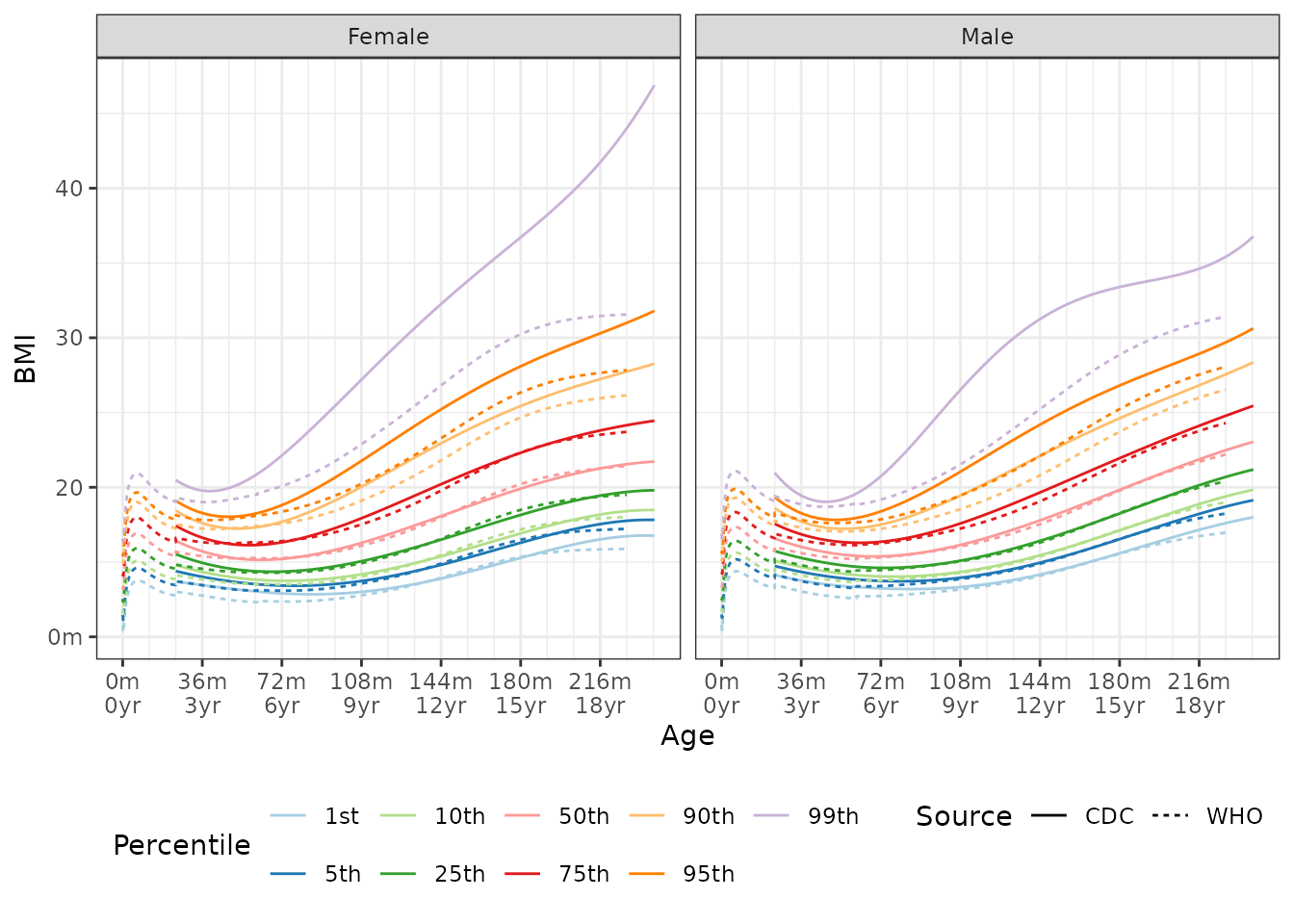
The median BMI quantile for a 48 month old female is:

q_bmi_for_age(p = 0.5, male = 0, age = 48) # default is CDC
## [1] 15.32168
q_bmi_for_age(p = 0.5, male = 0, age = 48, source = c("CDC", "WHO"))
## [1] 15.32168 15.26020

A BMI of 17.2 for a 149 month old male is in the following percentiles by source:

p_bmi_for_age(q = 17.2, male = 1, age = 149, source = c("CDC", "WHO"))
## [1] 0.3533024 0.3787698

If you would prefer to have the z-score for a BMI of 17.2 for a 149 month old male is in the following percentiles by source:

z_bmi_for_age(q = 17.2, male = 1, age = 149, source = c("CDC", "WHO"))
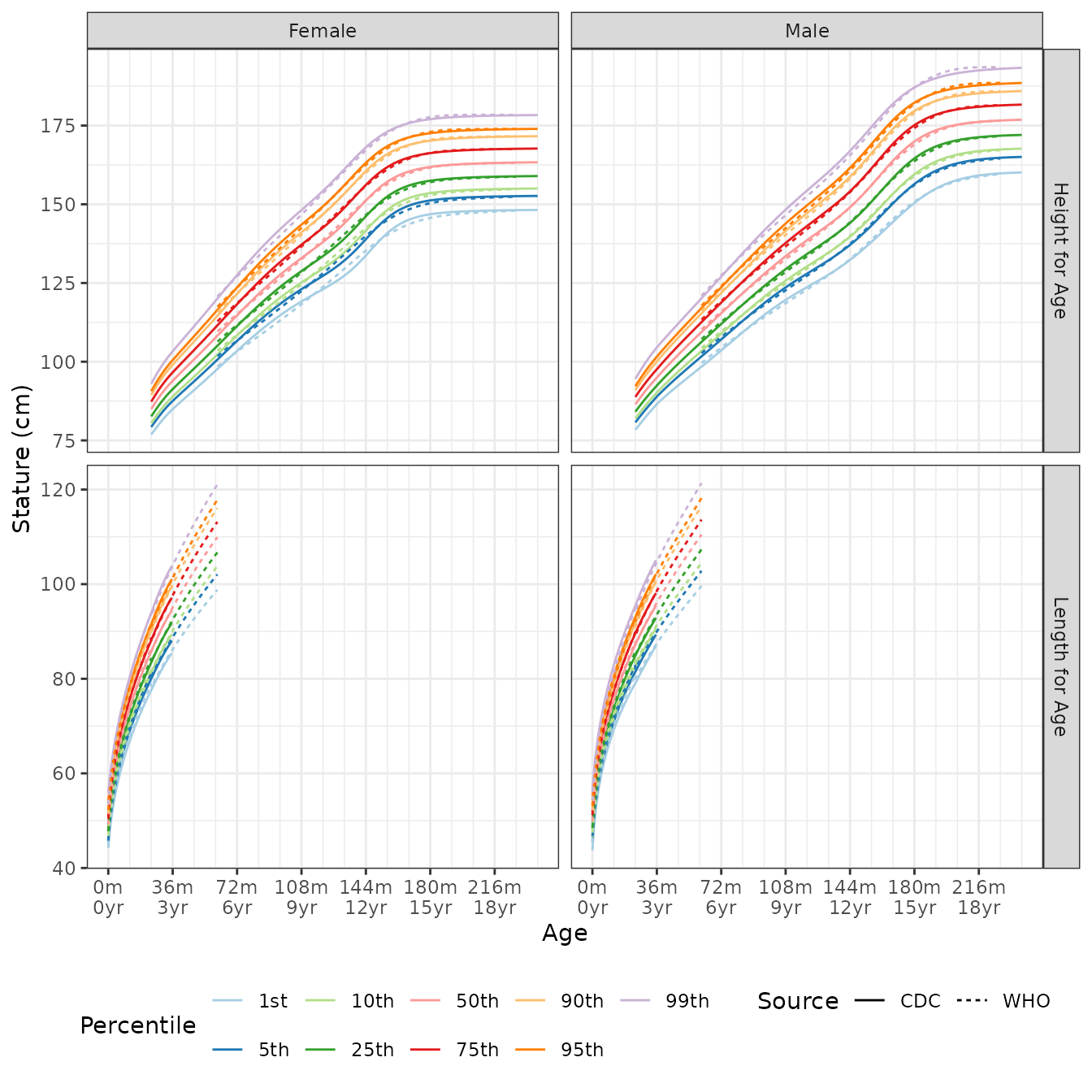
## [1] -0.3764197 -0.3087132

Head Circumference for Age

Stature for Age

Stature is either height or length. Functions for both are provided.

The image below is the growth chart by data source and by height or length.

The following image shows the difference in the quantile values between height and length for the same age.

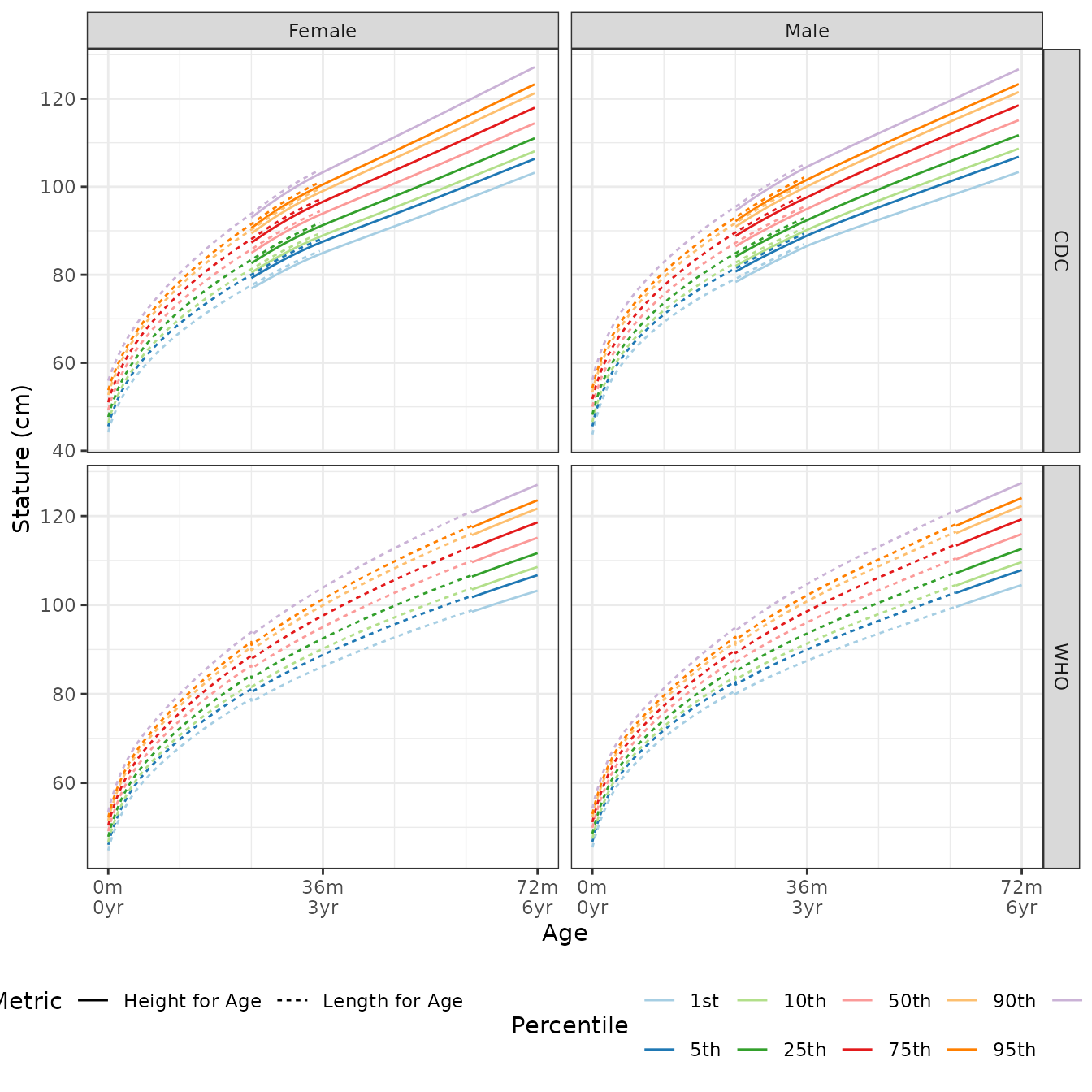
Length for Age

Length for age quantiles are found via q_length_for_age. For example, the median length for a 1.5 year old male, based on CDC data is:

q_length_for_age(p = 0.5, age = 1.5 * 12, male = 1, source = "CDC")
## [1] 81.44384

A 90 cm long 28 month old female is in the 63th percentile:

p_length_for_age(q = 90, age = 28, male = 0, source = "CDC")
## [1] 0.628035

or the equivalent z-score:

z_length_for_age(q = 90, age = 28, male = 0, source = "CDC")
## [1] 0.3266536

Height for Age

Height for age quantiles are found via q_height_for_age. For example, the median height for a 11 year old male, based on CDC data is:

q_height_for_age(p = 0.5, age = 11 * 12, male = 1, source = "CDC")
## [1] 143.3107

A 125 cm tall 108 month old female is in the 10th percentile:

p_height_for_age(q = 125, age = 108, male = 0, source = "CDC")
## [1] 0.1008541

or the equivalent z-score:

z_height_for_age(q = 125, age = 108, male = 0, source = "CDC")
## [1] -1.2767

Weight for Age

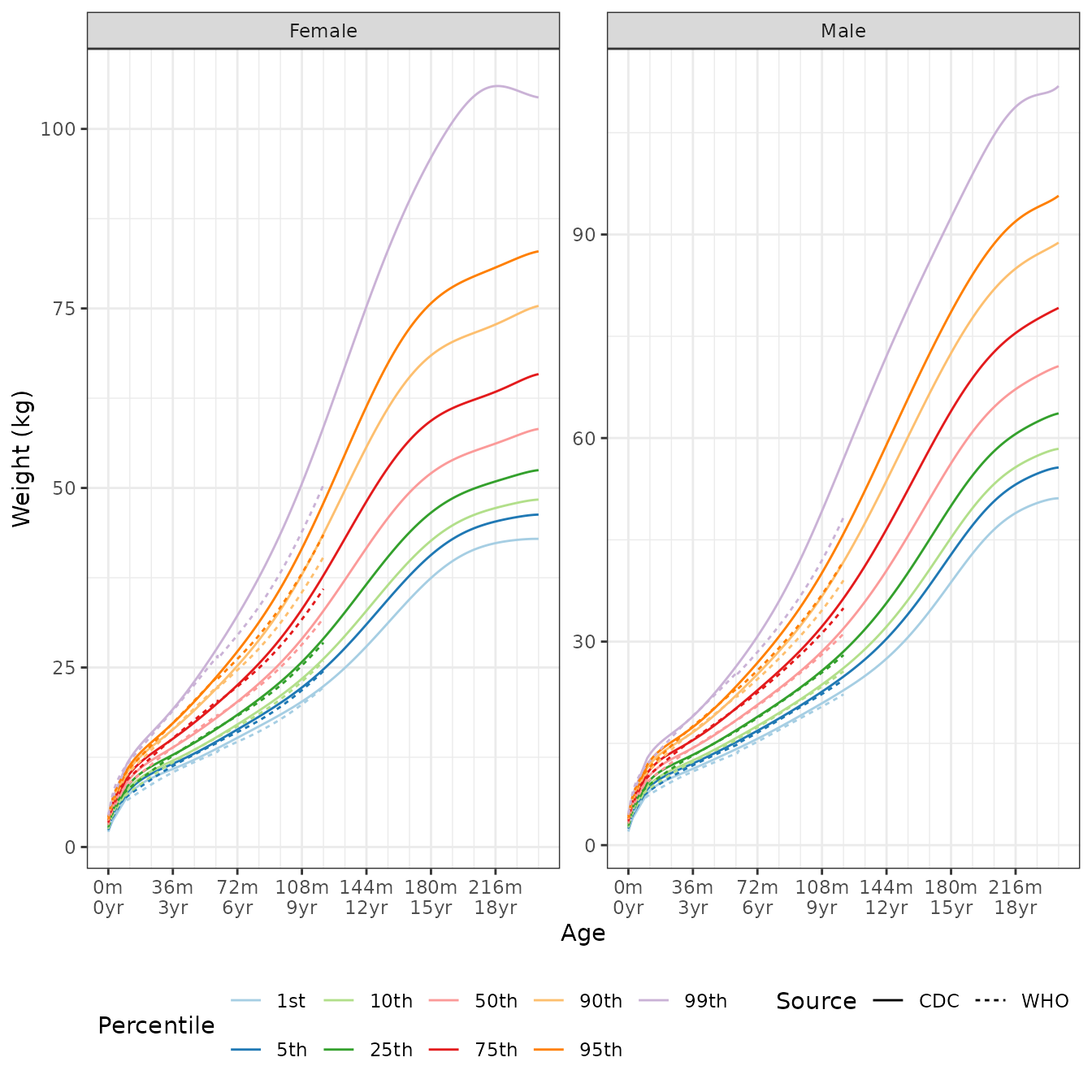
Find the 80th quantile for 56 month old females

q_weight_for_age(p = 0.80, age = 56, male = 0, source = c("CDC", "WHO"))
## [1] 19.38674 19.84028

The percentiles for 42 kg 9 year old males:

p_weight_for_age(q = 42, age = 9 * 12, male = 1, source = c("CDC", "WHO"))
## [1] 0.9666286 0.9900309
z_weight_for_age(q = 42, age = 9 * 12, male = 1, source = c("CDC", "WHO"))
## [1] 1.833402 2.327507

Weight for Stature

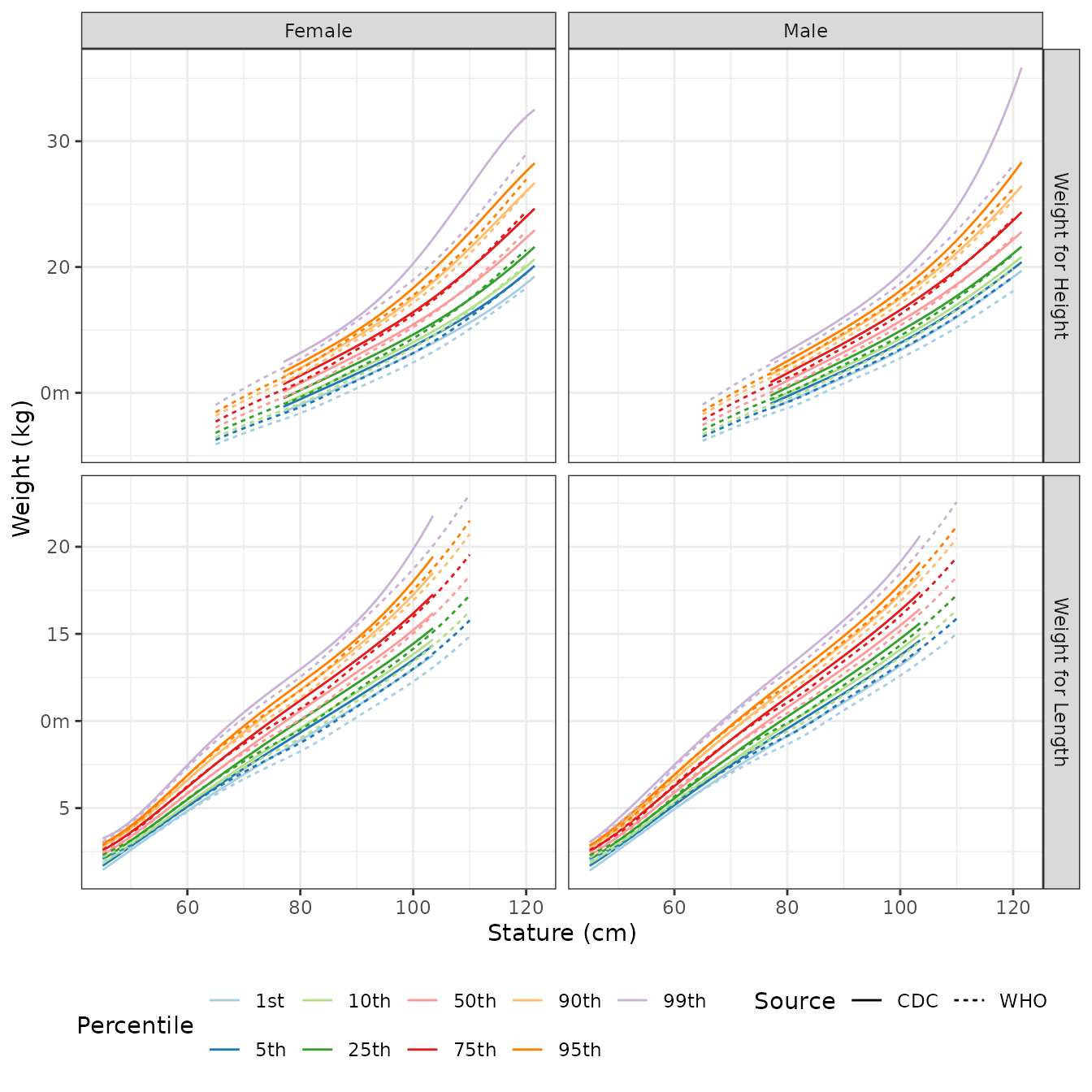
The 60th weight quantile for a 1.2 meter tall male is

q_weight_for_height(p = 0.60, male = 1, height = 120, source = "CDC")
## [1] 22.4941
q_weight_for_height(p = 0.60, male = 1, height = 120, source = "WHO")
## [1] 22.89542

There are slight differences in the quantiles for length and height

q_weight_for_length(p = 0.60, male = 1, length = 97, source = "CDC")
## [1] 14.88168
q_weight_for_height(p = 0.60, male = 1, height = 97, source = "WHO")
## [1] 14.85803

q_weight_for_length(p = 0.60, male = 1, length = 97, source = "CDC")
## [1] 14.88168
q_weight_for_length(p = 0.60, male = 1, length = 97, source = "WHO")
## [1] 14.6771

Percentiles and standard scores for a 14 kg, 88 cm tall/long male

p_weight_for_height(q = 14, male = 1, height = 88, source = "CDC")
## [1] 0.9003879
p_weight_for_height(q = 14, male = 1, height = 88, source = "WHO")
## [1] 0.9285045
p_weight_for_length(q = 14, male = 1, length = 88, source = "CDC")
## [1] 0.9277451
p_weight_for_length(q = 14, male = 1, length = 88, source = "WHO")
## [1] 0.9479553

Corresponding standard scores

z_weight_for_height(q = 14, male = 1, height = 88, source = "CDC")
## [1] 1.283765
z_weight_for_height(q = 14, male = 1, height = 88, source = "WHO")
## [1] 1.464743
z_weight_for_length(q = 14, male = 1, length = 88, source = "CDC")
## [1] 1.459201
z_weight_for_length(q = 14, male = 1, length = 88, source = "WHO")
## [1] 1.625343